Laboratoires de Mathématiques

Propositions de thèmes pour les laboratoires en lycées

Le laboratoire IMAG et l’IREM participent à la création et aux activités des Laboratoires de Mathématiques des lycées de l’académie.
De nombreux chercheurs ou enseignants-chercheurs ont accepté de proposer des thèmes pouvant intéresser les membres des laboratoires de mathématiques et correspondant à leurs goûts ou activités de chercheurs.
Pour chacun de ces thèmes, l’intervenant pourra préparer une ou plusieurs rencontres.
Les modalités précises de ces interventions — horaires, types d’activité (exposé, atelier, discussion), etc — seront définies au cas par cas.

La liste suivante n’est pas exhaustive, n’hésitez pas à proposer vos propres thèmes !
Contact : thierry.mignon@umontpellier.fr

Vous trouverez sous format pdf la liste des thèmesici.

Le diaporama de la présentation du 5 février 2018ici.

Liste des thèmes :

1. Symétries en physiques et lois de conservation, proposé par Philippe Roche

La théorie des groupes implémente la notion de symétrie qui est centrale en physique fondamentale comme par exemple les quantités conservées en mécanique classique, la Relativité et le groupe de Lorentz ou la Mécanique quantique et le groupe des transformations unitaires. Le projet sera centré autour de la notion de groupe et de ses représentations et d’une application transversale sur un sujet de physique où les symétries jouent un rôle essentiel.

2. Mathématiques et algorithmiques pour l’analyse de la variabilité de surfaces corticales issues de la segmentation d’IRM, proposé par : Benjamin Charlier

La démocratisation de l’imagerie par résonance magnétique (IRM) rend nécessaire l’automatisation de l’analyse de la variabilité des données acquises. Ainsi, pour tenter d’améliorer la détection des maladies neuro-dégénératives (type Alzheimer ou Parkinson), un des champs de recherche actuel, concerne l’étude des changements de conformation de certaines structures cérébrales au cours du temps. En clair, on se pose la question suivante: comment déterminer, à partir d’une base de données d’apprentissage (en pj un exemple d’évolution temporelle pour un patient suivi sur 10 ans), si un changement de forme de l’hippocampe est d’origine pathologique ou est dû au vieillissement normal ? Partant d’exemples de données réelles, nous présenterons des techniques allant des outils théoriques (géométrie riemannienne, analyse Hilbertienne) aux outils plus pratiques (méthodes numériques, différentiation automatique, apprentissage machine) pour traiter ces données de grande dimension. L’ensemble des notions abordées pouvant être assez vaste, la discussion pourra (devra) se concentrer sur certains sujets en accord avec l’intérêt des participants.

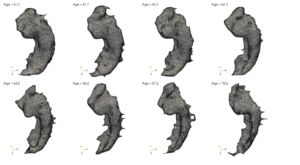
Mots-clés : analyse de forme, géométrie, statistique, apprentissage, calculs massivement parallèle.

 3. Introduction aux mathématiques du choix collectif, proposé par Xavier Bry et Nicolas Saby

L’outil principal d’expression collective en démocratie, c’est le vote. Or, on peut montrer, avec des outils mathématiques assez simples, que les systèmes classiques dysfonctionnement complètement, et comment on peut y remédier. On proposera dans cet atelier un périple constellé d’exemples allant des fondations mathématiques du choix collectif (18ème siècle) jusqu’aux théorèmes d’impossibilité (20e siècle) et à leur possible de contournement (21e siècle).

4. Promenade : des marches aléatoires à l’équation de la chaleur, proposé par Jérémie Brieussel

Sur une grille quadrillée, une marche aléatoire est la trajectoire décrite par une particule qui à chaque croisement décide de sa direction (Nord-Sud-Est-Ouest) au moyen d’un dé tétraédrique régulier. On peut déjà se poser plusieurs questions sur les marches aléatoires. A quelle distance de son point de départ se trouve la particule à un temps t donné ? Quelle est la probabilité que la particule soit de retour à son point de départ à ce temps t ? Pour une grille quadrillée bidimensionnelle, un théorème de Polya assure qu’avec probabilité 1 la particule repasse par son point de départ une infinité de fois. Par contre, dans une telle grille tridimensionnelle, ce phénomène a lieu avec probabilité 0.
D’autre part les marches aléatoires sont liées à l’équation de la chaleur discrète, où à chaque unité de temps, la ”chaleur” d’un site se répartit uniformément sur les sites voisins. Ce lien est intuitif si l’on imagine la chaleur comme une grande quantité de ”particules caloriques”.
Enfin, si les mailles de la grille sont suffisamment petites (ou si on regarde de suffisamment loin), la trajectoire de la particule décrit le fameux mouvement brownien, lié comme précédemment à l’équation différentielle de la chaleur.

5.Mathématiques Discrètes,proposé par Jorge Ramirez-Alfonsin

La méthode probabiliste est un outil puissant qui a été utilisé pour aborder beaucoup de problèmes dans les mathématiques discrètes. Nous regarderons le fonctionnement de cette méthode avec un problème sur les tournois (graphe complet orienté). Si le temps le permet, nous discuterons également le problème connu comme le dilemme de l’espion. Nous décrirons une méthode (basée sur la notion de 3-colorations d’un graphe) pour échanger des mots de passe dans le contexte du dilemme.

6. Mathématiques Babyloniennes,proposé par Anne Cortella.

Compter en base 60 comme les babyloniens c’est facile. Mais que savaient-ils vraiment faire ?
En se basant sur les travaux de Christine Proust, historienne des maths, qui a étudié les tablettes d’argile trouvées à Nippur, on peut s’interroger sur les nombres et les méthodes de calcul, mais surtout sur la manière de les représenter et de les penser. De quoi retourner faire de l’arithmétique.

7. Relation d’Euler et conjecture de Poincaré,proposé par Thierry Mignon

La relation d’Euler affirme que pour tout polyèdre usuel (dés à plusieurs faces, polyèdres platoniciens entre autres), le nombre de sommets, moins le nombre d’arêtes, plus le nombre de faces est toujours le même.

Nous pourrions aborder l’origine de cette formule et tenter de proposer des idées de preuves. L’histoire de cette preuve est émaillée de démonstrations incomplètes ou fausses, qui conduisent à la notion de genre d’une surface.

Nous pourrons aussi parler de la conjecture de Poincaré et des problèmes du prix du millénaire.

8. Autour de la théorie des nœuds, proposé par Hoel Queffelec

Un nœud au sens mathématique, c’est la même chose qu’un vrai nœud dans la vraie vie : une ficelle nouée. Simplement, on en recolle les deux bouts. Se pose alors la question de distinguer les nœuds à déformation près. Cette question vieille de plus d’un siècle a largement alimenté toute une part de la géométrie et de la topologie, et pourrait donner lieu à un atelier, autour de la représentation des nœuds, de leurs invariants polynomiaux, voire des outils de catégorification diagrammatique qui leur sont reliés.

9.Jeux combinatoires, proposé par David Théret

Les jeux combinatoires sont des jeux à deux joueurs, sans hasard et à information totale. La plupart des jeux ”sérieux” classiques en sont des exemples (échecs, dames, go…) Une classe particulière de jeux combinatoires, dont le jeu de Nim est le représentant de référence, est particulièrement simple à analyser. Leur étude ne demande aucun prérequis, et fait essentiellement appel au raisonnement logique ; elle peut se pratiquer à tout niveau (de l’école élémentaire à l’université, avec évidemment des objectifs différents).

10. Algorithmique,proposé par Simon Modeste

L’algorithmique prend une place importante dans les programmes du secondaire. La proposition peut concerner un approfondissement sur l’algorithmique (complexité, algorithmes avancés, structures de données spécifiques, etc.) ou une intervention plus liées aux questions d’enseignement et d’apprentissage de l’algorithmique, en lien avec les mathématiques. Formule à préciser avec les enseignants concernés.

11. Mathématiques, bulles de savon et isopérimétrie, proposé par Philippe Castillon

Nous aborderons quelques questions autour de la géométrie différentielle, en particulier sur la notion de surfaces, les différentes notions de courbures et quelques problèmes d’optimisations de formes ou d’énergie en géométrie (par exemple, la notion de surface minimale qui permet de retrouver la forme des films de savons).

12. Équations différentielles et modélisation, proposé par Pascal Azerad

Les lois physiques ou biologiques s’écrivent souvent en équations différentielles.
Sous forme d’atelier, on cherchera à visualiser les équations différentielles, à en calculer des solutions exactes ou approchées, à la main ou avec un ordinateur.

13. La fleur de tournesol, proposé par Jean Malgoire

L’observation attentive d’une fleur de tournesol par sa mystérieuse beauté, nous met immédiatement au défi, pour peu que l’on ait un minimum de curiosité scientifique, d’en comprendre la structure complexe. Plusieurs approches sont possibles mais toutes nous conduisent, à travers différents modèles, vers le nombre d’or et la théorie des fractions continuées. L’exploration de quelques modèles ainsi que l’étude de la théorie des fractions continuées constitue le cœur du thème proposé.

14. Simulation numérique pour les écoulements sanguins, proposé par Simon Mendez

Depuis mon recrutement au CNRS en 2010, je travaille sur l’application des mathématiques appliquées au champ de la simulation numérique des écoulements sanguins. Les problématiques sont très variées, car mes travaux portent à la fois sur les écoulements sanguins dans les grands vaisseaux du corps (grandes artères et cœur) et sur les écoulements sanguins à l’échelle même des globules rouges. Je peux donc présenter la simulation numérique en mécanique des fluides, parler de résolution d’équation par ordinateur, et des applications au médical. Qu’est-ce que les maths/la simulation permet d’apprendre au médecin ? En quoi peuvent-elles servir pour l’ingénierie biomédicale ? Voici des exemples d’application : explication des mouvements du sang dans le corps ; prévision de la coagulation du sang ; simulation de dispositifs biomédicaux (valves artificielles, dispositifs de traitement d’anévrismes…) ; amélioration des analyses de sang ; compréhension de la rhéologie du sang ; lien entre état de la membrane des globules rouges et leur comportement en écoulement ; simulation d’imagerie médicale.

15. Fonctions et topologie de la droite réelle, proposé par Viviane Durand-Guerrier

Deux ateliers, à faire séparément, ou au cours d’une seule rencontre.

• Étude des points fixes d’une fonction croissante d’un ensemble dans lui-même

Dans cet atelier, on proposera aux participants de questionner l’existence de points fixes pour une fonction croissante d’un ensemble dans lui-même dans différents ensembles de nombres.
L’objectif de cet atelier est de questionner les distinctions entre le discret le dense et le continu pour les ensembles usuels de nombres.

• Construction de fonctions vérifiant la relation algébrique   ƒ(a+b) = ƒ(a) ƒ(b)

Dans cet atelier, on proposera aux participants d’explorer les fonctions vérifiant cette relation algébrique pour une valeur donnée de ƒ(1) en se plaçant dans N  , dans Z, dans Q puis dans R.
L’objectif de cet atelier est de questionner les distinctions entre le discret le dense et le continu pour les ensembles usuels de nombres.

16. Fractions continues, approximation des réels par des rationnels et statistiques, proposé par Alain Bruguière

Vous trouverez le texte de cette proposition sur le document pdfici.

17. Mathématiques de l’informatique, proposé par Simon Modeste

L’algorithmique prend une place importante dans les programmes du secondaire.
La proposition peut concerner un approfondissement sur l’algorithmique (complexité, algorithmes avancés, structures de données spécifiques, etc) ou une intervention plus liées aux questions d’enseignement et d’apprentissage de l’algorithmique, en lien avec les mathématiques. Formule à préciser avec les enseignants concernés.

18. Le vrai et le démontrable : vers les théorèmes de Gödel, proposé par Jean Malgoire

Depuis la création par Euclide, il y a plus de 23 siècles, de la méthode axiomatique, la distinction entre ces deux notions est progressivement devenue nécessaire et éclairante sur la nature (du point de vue logique) de l’activité mathématique. La VERITE d’un énoncé n’a de pertinence que dans chaque modèle particulier d’une théorie axiomatique (donc du côté du champ sémantique) alors que la PREUVE de ce même énoncé est une notion syntaxique ne dépendant que des axiomes de la théorie et des méthodes de démonstration fixées. Une approche élémentaire de cette distinction peut être faite à partir de théories axiomatiques très simples comme celle de la géométrie plane affine (dans l’esprit d’Euclide…) où la variété des modèles (par exemple des plans affines sur des corps finis) nous fournit des exemples très naturels de formules indécidables (c.à.d. formules telles que ni elles ni leurs négations ne peuvent être démontrées.) On pourra ensuite aller plus loin en s’intéressant à des théories axiomatiques justement célèbres comme l’arithmétique de Peano ou la théorie des ensembles, et par la même occasion arriver à une compréhension raisonnable des théorèmes de Gödel.

19. Cryptographie, arithmétique et informatique, proposé par Thierry Mignon

Jeu, ou enjeu stratégique, le cryptage de document est une activité ancienne. Jules César cryptait ces communications en décalant chaque lettre de trois crans. Depuis l’arrivée d’Internet, des transferts de fichier et de la généralisation des transactions en lignes, la cryptographie est devenue une activité essentielle de nos sociétés. Les dernières méthodes de chiffrement reposent sur des résultats récents de théorie des nombres, et des algorithmes informatiques toujours plus performants. Nous pourrons évoquer ensemble, et peut-être programmer à l’aide du logiciel Sage, les premières de ces méthodes à clé publiques ou privées, dont la méthode RSA.

20. La mesure des aire d’Archimède à Lebesgue, proposé par Gaëtan Planchon

Dans cette atelier, nous explorerons la notion d’aire. En commençant par la méthode d’exhaustion d’Archimède et le calcul de l’aire du disque et du segment de parabole, nous discuterons des indivisibles de Cavalieri qui précèdent le calcul infinitésimal. Nous poursuivrons la question de la mesure des aires avec la construction d’une mesure des ensembles quarrables du plan, ce qui fournit une théorie pour l’introduction de l’intégrale en Terminale S. Ce travail pourra se prolonger par une construction de la mesure de Lebesgue des compacts du plan, puis des ouverts.
Un deuxième atelier pourra être proposé pour _étudier les procédures intégrales et différentielles entre mathématiques et physique (découpage, sommation, limite).

21. L’histogramme, de la statistique descriptive à la statistique inférentielle, proposé par Elodie Brunel-Piccinini

L’histogramme est un objet à la fois très populaire et mal connu. Chacun a déjà été confronté à cette représentation graphique qui se résume bien souvent en une juxtaposition de rectangles dont l’aire est proportionnelle ou égale à la fréquence des classes dans lesquelles sont rangées les observations. Mais cet objet prend tout son sens dès lors que l’on considère les observations comme réalisations de variables aléatoires dans un modèle d’échantillonnage. L’histogramme devient alors lui-même une variable aléatoire, estimateur de la densité de probabilité sous-jacente au modèle aléatoire, dont on peut _étudier les propriétés probabilistes. Sous cet angle, il est alors possible d’établir un lien entre la statistique descriptive et la statistique inférentielle.

22. D’autres thèmes

Les thèmes suivants ne sont pas associés à un intervenant précis, mais pourraient être abordés avec l’un des membres de l’IMAG.

• L’infini et les cardinaux.
• Systèmes dynamiques, problèmes des trois corps ou théorie du chaos.
• Utilisation du traitement de texte LaTeX
• Utilisation de logiciels de statistiques.
• Utilisation du logiciel de calcul formel SAGE
• Discussions sur les théorèmes ou conjectures célèbres (les prix du millénaire, le théorème de Fermat, etc…)
• !